Unlocking the Defensive Code: Exploring the Impact of Physical Attributes on NBA Rookie Defense
- Bruin Sports Analytics

- Apr 1, 2024
- 5 min read
By: Soomedha Vasudevan and Nick Chu
Introduction
With the NBA playoffs just around the corner and only a handful of games remaining in the regular season, basketball fans eagerly anticipate which players will rise to the top. In this analysis, we aim to explore the key traits that distinguish top-performing players and determine their impact on team success.
Our central question is: Are physical attributes indicative of defensive stats for rookies in the league? To answer this, we will analyze the data collected during the NBA rookie combine and their respective performances in their rookie seasons. Using machine learning and visualizations, we aim to predict which players will carry their team in this season's playoffs. While many fans speculate about physical attributes like height and wingspan in basketball, our analysis seeks to uncover a number-based relationship between player statistics and these traits. By analyzing attributes and their correlation with defensive statistics such as steals, blocks, and rebounds, we aim to identify the most influential factors driving success on the court. Ultimately, our analysis is motivated by a desire to reveal the role of physical attributes in defensive maneuvers and their impact on team performance.
Analysis
We will categorize players and their statistics based on their positions, such as Center, Power Forward, Small Forward, Shooting Guard, and Point Guard. This will help minimize confusion and allow for targeted analysis of the impact of traits on each position and the following contribution to team performance.
Initially, we thought that wingspan would play an influential role in player performance and defensive statistics. To minimize height as a confounding variable, we decided to use the ratio of wingspan over height so that it does not take into account differences in height as much. We compared this to the data regarding steals. Steals would be highly correlated with wingspan to height ratio because a longer wingspan relative to height can indicate greater reach and potential to disrupt passing lanes, intercept the ball, and tip passes, all of which are key factors in accumulating steals. Additionally, a longer wingspan could provide an advantage in contesting shots and overall defensive presence, further influencing steal opportunities. Thus, analyzing the relationship between wingspan to height ratio and steals can provide insights into how physical attributes impact defensive performance. As a note, we categorized the stats all on a per-36 basis and only included rookies who played at least 10 minutes per game.

However, we noticed that there were not any strong correlations present in the scatter plots. This led us to believe that there might be other factors more influential in steal performances. All of the graphs seem to be a random scatter without any strong linear, positive or negative, correlations.
Another comparison that was inferred to be statistically significant was the correlation between height (in inches) and blocks. This is because taller players typically have longer wingspans and greater reach, which can make it easier for them to block shots. Taller players also tend to have a higher standing reach, allowing them to block shots without necessarily having to jump as high as shorter players. Additionally, taller players often have greater strength and physical presence, which can make it more challenging for opposing players to shoot over them or drive to the basket without being blocked. Therefore, analyzing the relationship between height and blocks can provide insights into the impact of height on defensive performance and shot-blocking abilities.

However, once again no strong trends were to be found. The strongest correlation was for point guards, which makes sense since taller point guards may have longer arms and greater reach, allowing them to contest shots and block attempts more effectively.
The last comparison that we felt was relevant was height against defensive rebounds. We inferred this would have a strong correlation since height often correlates with a player's ability to reach higher for rebounds, giving them an advantage over shorter players. This seemed like it would have a clear association.

Once again, there were no strong correlations. There seems to be a wide range of defensive rebound statistics for all height rangers. This implies that defensive rebounds do not rely on height.
Overall, our scatter plots were unimpressive in terms of showcasing strong patterns or indicators of correlations. However, this does not mean that player statistics are completely isolated from their body measurements. This just indicates that there are no strong correlations between separate traits with separate skills.
Model
Our goal for evaluating a model is to see if wingspan, height, weight, and wingspan to height ratio can be used as predictor variables to create accurate predictions for a player’s defensive stats, that being rebounds, blocks, and steals. We used a Random Forest Regressor model in order to perform regression on our data, and trained the model on an 80/20 train test split using the previously listed variables as the X and y. Additionally, we performed feature selection to try to select the most optimal features for the model, and it coincidentally turned out to be using all 4 of the attributes to make predictions. From there, we trained the model and made predictions on the test set.
Evaluating the test set on different evaluation metrics saw us getting a mean absolute error of 0.594, meaning the model’s predictions were 0.594 off from the actual values for rebounds, blocks, and steals. Additionally, we got an R-squared value of 0.366, indicating that 36.6% of the variance of the rebounds, blocks, and steals could be explained by the physical attributes we chose. These results are encouraging as it is clearly better than blindly guessing but leaves lots of room for improvement. We also looked at training the model to solely predict each of the 3 defensive stats, rebounds, blocks, and steals, as a single target variable instead of all three being predicted at once. We only saw encouraging results when using rebounds as the sole target variable, where we improved the R-squared value to 0.586.
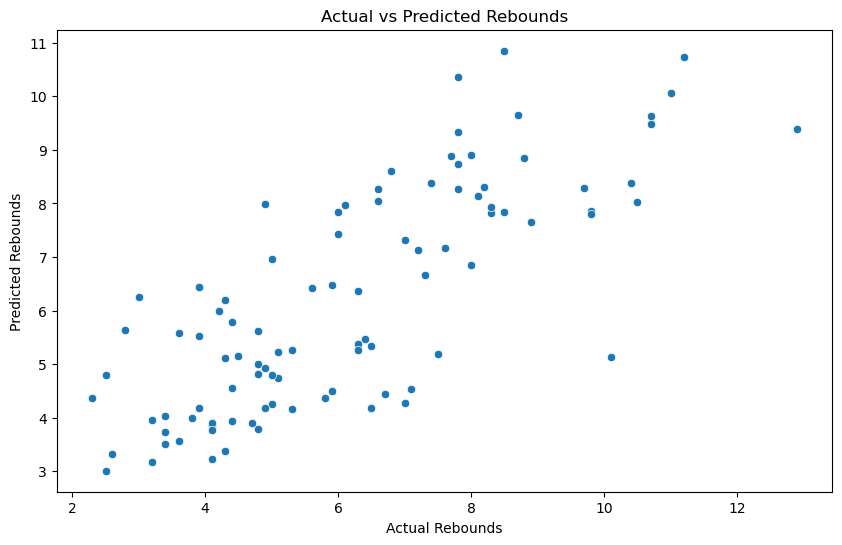
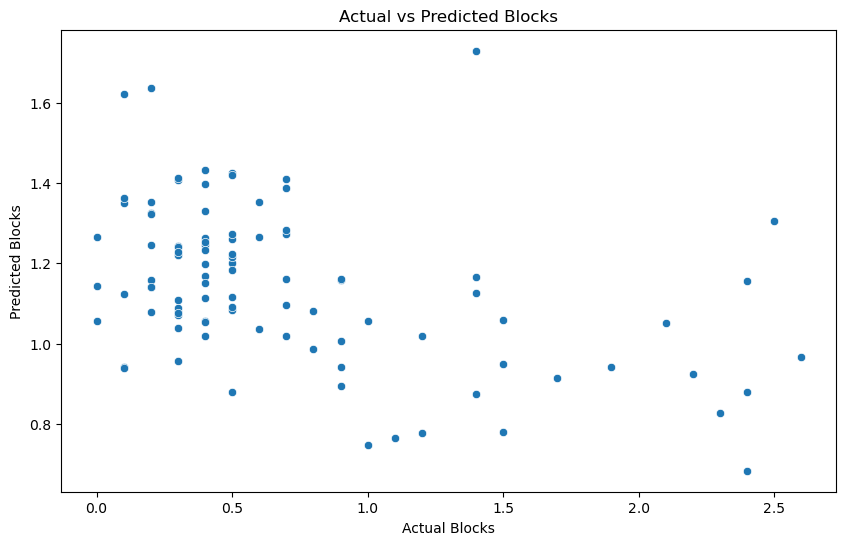
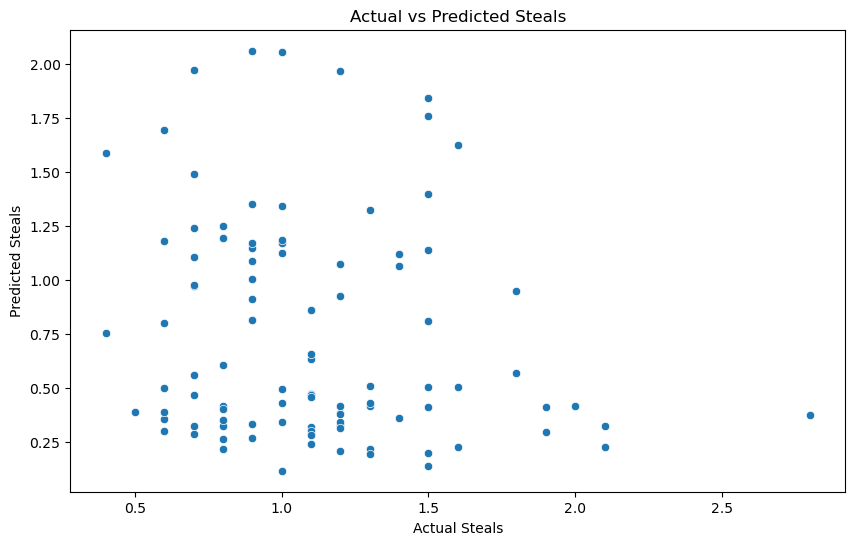
In order to better visualize how accurately the models were predicting each of the defensive stats, we created 3 scatterplots for rebounds, blocks, and steals. Within each of these scatterplots, we plotted the players’ actual recorded defensive stat on the x-axis and the players’ predicted defensive stat from the model on the y-axis. This means that if the model has good predictive power, then the points in the scatterplot should line up in a straight line with a slope of 1, as all the coordinates on the x and y axis should be the same. We see the results below.
We can see from these scatterplots that our previous analysis indicating that predictive power went up when only considering rebounds was rooted in truth. We can clearly see that the rebounds scatterplot has a stronger positive correlation than the other stats’ plots. The other scatterplots do not offer much insight unfortunately, as it seems the model cannot make the most accurate predictions solely based on the physical attributes we provided it.
Conclusion
We initially believed that certain physical attributes would correlate with certain defensive stats. For example, wingspan would naturally correlate with steals, as a player with a longer wingspan would be able to poke at the ball more often with effectiveness. However, our model gave us results that indicated that for steals and blocks, the physical attributes we provided were not sufficient enough for the model to make accurate predictions. This does make sense, as there is so much more to defense than physical tangibles: the intangibles are arguably more important for a lot of players. Draymond Green is 6’6”, yet he is one of the greatest defenders of all time for example. But our model is not necessarily worthless, as we did find that the predictive power was higher when looking at rebounds. So in conclusion, generally when looking at rookies, one should look with caution when solely considering physical attributes to predict their defensive prowess, as many other qualities of a player are important to consider as well.



Comments